TL;DR
This article reframes first-principles thinking in a practical light, emphasizing the need to not only break down problems but also understand the relationships between sub-problems and solutions. Using personal insights and a football analogy, it highlights how decomposition, relationship appreciation, and solution recombination are critical to effective problem-solving. It also discusses the limitations of first-principles thinking and how it should be complemented by other tools when necessary.
This article will not try to tell you anything that you do not already know. For all it is worth, it will take a simple idea that you must have heard a countless number of times and try to present it in a more practical light.
Let me start by telling you a short story.
Some months ago, Sandeep and I were taking a business class titled “The Strategy and Management of Technology Innovation”. It was one of those classes in which someone could answer a question with a five-minute long diatribe on a company’s leadership about their failure to innovate without mentioning for once what it meant to innovate (in this particular context); there was always an immensity of speech, but a dearth of substance. If I randomly woke up from sleep and the teacher called you up to answer a question you did not hear, all you had to do was say, “the company should innovate and diversify their product offerings”, and chances are very high that your answer will be passable. One faithful day, on our way back from class, Sandeep convinced me that such platitudes about givens like innovation and diversification were an educated waste of our precious time. He suggested, and I agreed, that there was more value to be added if we made suggestions that were evidence of innovation without explicitly mentioning innovation; to say that a company needed to innovate (at least in the context of our class) was a tautology.
My friend Sandeep was making a very powerful statement: for frameworks to be useful, we have to operationalize them.
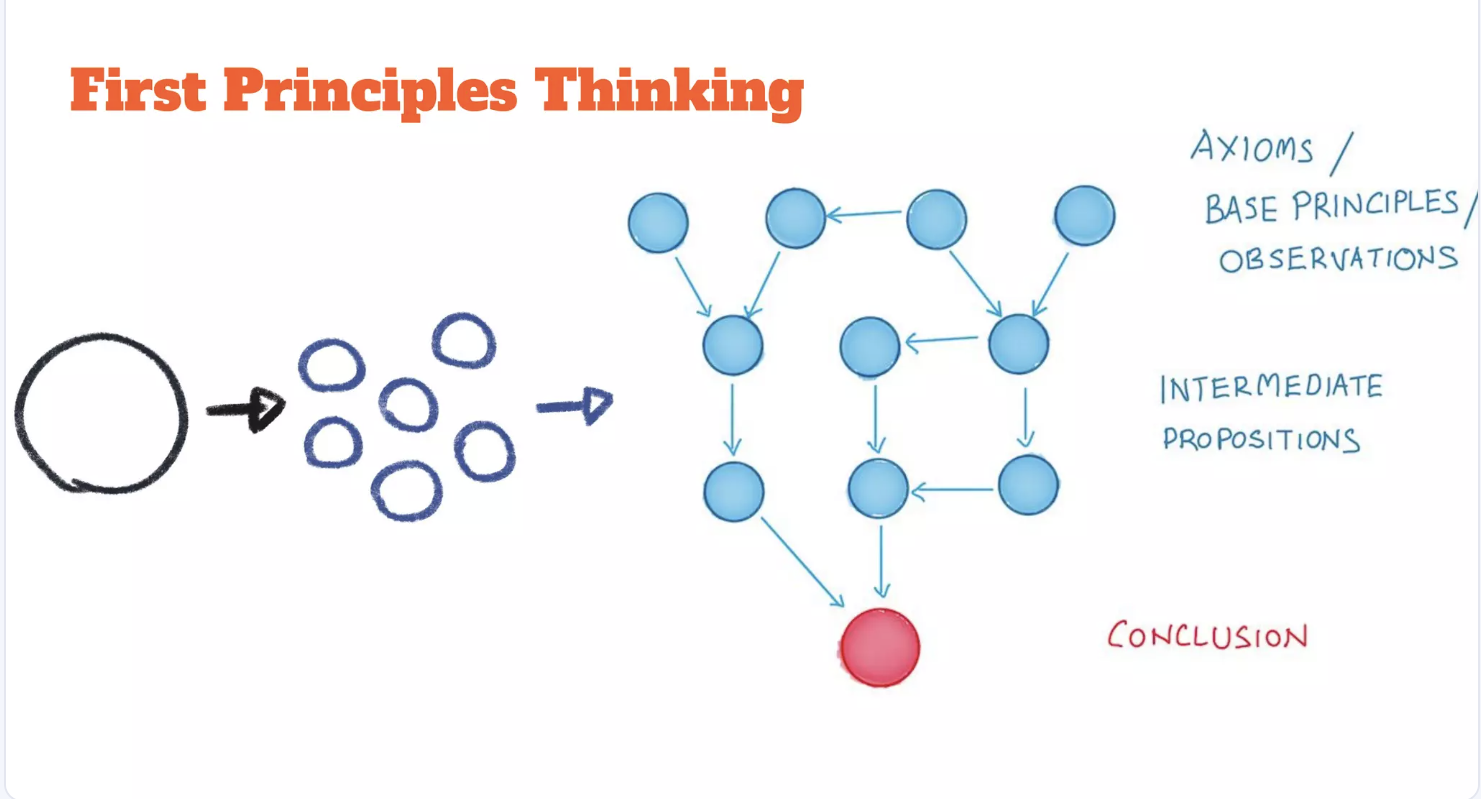
Let us consider the idea of problem solving from first-principles. It is all too common these days to hear an exposition on the virtues of first-principle thinking; but what does that really mean? What does it mean in relation to how we must organize our learning to enhance our problem solving capabilities?
To enable a first-principles thinking approach to learning, we must emphasize a learning approach that emphasizes (1) the importance of identifying and appreciating the strength of relationships, (2) correctly decomposing complex problems into mini-problems, (3) developing the agility to learn what it takes to solve mini-problems (sometimes in a recursive manner), and (4) the tact to combine the solutions to our mini-problems in a way that correctly solves the initial problem.
Each of the four highlighted phases is as important as they come. Of all four, we can argue that identifying and appreciating the strengths of relationships is the most important as it enables and facilitates both the decomposition and combination phases. To start with, if we cannot fully grasp the relationships that define our problem, we cannot correctly decompose the problem. And correct decomposition is important; if one falls short of it then there cannot be any first principles to begin with, and if one unnecessarily goes above and beyond then they must have created a problem that is bigger than and hence different from the original problem. Once decomposed, solving the “first-principle problems” is clearly the heart of the process and there is no need to belabor the point. After solving these mini-problems (first-principle problems), however, we have to use our understanding of the relationships that govern the whole problem space and recombine the solutions to the mini-problems such that we are left with a solution to the initial problem.
The ability to solve the sub-problems is critical to first-principles thinking (it is in some sense the bottleneck). And while it is crucial that one develops the ability to solve decomposed problems, it is the ability to identify relationships (it is in some sense the rate determining step) that smoothens the iteration that is essential to effective problem solving.
We can use a very loose analogy of football to demonstrate the arguments above and in a broader sense an advantage of first-principles thinking approaches to problem solving, with the most obvious being that when we break down problems into a tree (in the computer science sense), we increase our search space for a solution by increasing the number of combinations that constitute the set of solution candidates.
We can break a game of football very loosely into a game for goalkeepers, defenders, midfielders and attackers. The sorry stories of numerous football clubs around the world have taught us that we cannot simply put in the best type of players in each category and fold our arms. The very first step, and the culprit in many stories, is a failure to begin by appreciating the relationships that define the game and the various positions, and then using that as an additional criteria for choosing which players are best for given positions. Once these players are chosen, we have to actualise the relationships to ensure that we actually have a football team that can win a game.
If one were asked to advise a struggling football team, the suggestion of even the most clearly thought out strategy will be just one strategy that may not leave the team able to perform desirable as conditions change. However, if one were to take into consideration what desirable performance is at every position, and the implications for the relationships that exist between the various solutions then one has a multitude of possible solutions among which the clearly thought out solution is only the best of many. The advantage of this decomposed exploration though, is that there has been an empowerment of the system to appreciate and embrace different solutions in different contexts.
Even after selecting the right players, successful teams continually adjust their strategy during the game, responding to emerging patterns on the field. These changing patterns reflect the changing dynamics of the problem, and only a team that has built an internal DNA for appreciating the relationships that exist on the pitch (an appreciation of the individual and collective strengths and weaknesses of the opposing team as well as of theirs), as well as the ability to promptly respond is poised to thrive.
With problem-solving as with football, effective first-principles thinking demands that in bringing to bear the powers of the individual theories/solutions that solve the sub-problems, we do not lose sight of the relationships that govern our activity. To lose sight of these relationships will be synonymous to trying to navigate the wide oceans without a knowledge of bearings.
With problem-solving as with football too, first-principles thinking requires constant adjustment as smaller problems are solved and new relationships become clear. It is more often than not an iterative approach operating in a dynamic setting, and one must exercise the same degree of vigilance that is expected of a ship captain in troubling waters.
If you are still reading this then you may have thought to yourself, “sometimes by its very nature this approach of breaking problems down and then combining solutions cannot solve a problem”, and o boy are you right! Not every problem lends itself to this approach to problem solving, and where a mere situational analysis will suffice, one can determine a priori that first-principles thinking alone will not suffice. Where a situational analysis fails to fully determine the effectiveness of first-principles thinking, it can be considered a tool that can complement other tools. Don’t always be in a rush to think from first principles.
It is also the case that even when the problem lends itself to a first-principles approach to problem solving, a combination (however well it is done)of the best solutions to the sub-problems does not yield the desired solution to the initial problem. In a bid to cater for the uniqueness of the sub-problems and the relationships that govern their combination, sometimes we must accept sub-optimal solutions to sub-problems to guarantee that the final solution is an appropriate response to the initial problem.
I hope that I did not say anything that you do not already know. I bet you already knew what first-principles thinking was about! I hope though, that now you can structure your learning in ways that allow you to appreciate relationships better, and consequently decompose problems and combine solutions with the sublimity of a master.
Thanks to Jesse-Jackson Zigi for reading drafts of this.